A typical example of diagrammatic proofs

Let’s assume we have four programs:

c₁ : B → C
c₂ : A → D
id : ∀ {T} T → T
swap₊ : ∀ {X Y} X + Y → Y + X

And two ways to “compose” programs:

_⊕_ : (A → B) → (C → D) → (A + C → B + D)
_⊙_ : (A → B) → (B → C) → (A → C)

We can now form four programs that are in some sense “equivalent”:

p₁ p₂ p₃ p₄ : (A + B) → (C + D)
p₁ = (c₂ ⊕ c₁) ⊙ swap₊
p₂ = swap₊ ⊙ (c₁ ⊕ c₂)
p₃ = (id ⊕ c₁) ⊙ swap₊ ⊙ (id ⊕ c₂)
p₄ = (c₂ ⊕ id) ⊙ swap₊ ⊙ (c₁ ⊕ id)

It means we can build bridges among these four “islands”:

It’s much clearer if I draw four “wiring diagrams” representing p₁ to p₄:

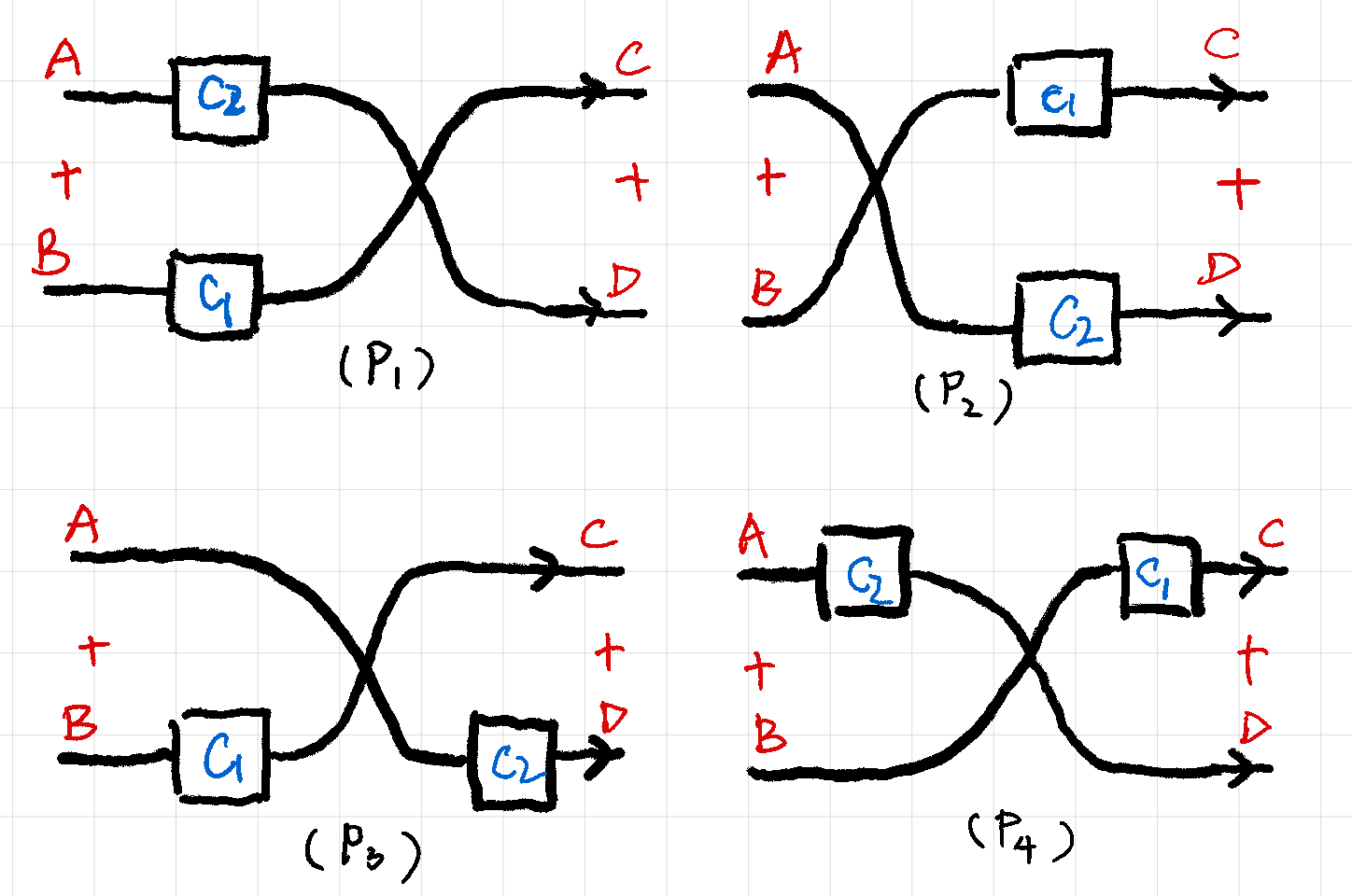
Now I can tell you that 1 rule of diagrammatic reasoning is enough to prove these equivalences:

Circuits can freely slide along wires.

Imagining in you mind!

Formal proofs for the very curious

In order to prove that p₁ p₂ p₃ p₄ are all equivalent “formally”, we need more than just 1 rule.

First of all, we need a rule with which we can prove p₁ ⇔ p₂ with zero effort:

swapr = (c₂ ⊕ c₁) ⊙ swap₊ ⇔ swap₊ ⊙ (c₁ ⊕ c₂)  -- it's called "double sliding"

Then we need a rule for “doing nothing”. It’s like a identity program transformation or identity proof:

_ = c ⇔ c

We also need two rules idl and idr, to “append” and “prepend” the identity program:

idl = c ⇔ id ⊙ c
idr = c ⇔ c ⊙ id

We need re-organize and associativity to perform “re-focusing” within proofs:

re-organize = (c₁ ⊙ c₂) ⊕ (c₃ ⊙ c₄) ⇔ (c₁ ⊕ c₃) ⊙ (c₂ ⊕ c₄)
associativity = (c₁ ⊙ c₂) ⊙ c₃ ⇔ c₁ ⊙ (c₂ ⊙ c₃)

Besides, we need two compositional rules _▣_ and _□₊_ to compose proofs of “sub-programs”.

_▣_ : 
    (c₁ ⇔ c₃) → (c₂ ⇔ c₄) →
    ---------------------------
    (c₁ ⊙ c₂) ⇔ (c₃ ⊙ c₄)
          
_□₊_ : 
    (c₁ ⇔ c₃) → (c₂ ⇔ c₄) →
    ---------------------------
    (c₁ ⊕ c₂) ⇔ (c₃ ⊕ c₄)

The formal proof of p₁ ⇔ p₃ is shown below:

p₁-p₃ : p₁ ⇔ p₃  -- it's called single sliding
  p₁-p₃ =
    begin₂
      (c₂ ⊕ c₁) ⊙ swap₊
    ⇔⟨ (idl □₊ idr) ▣ _ ⟩
      ((id ⊙ c₂) ⊕ (c ⊙ id₁)) ⊙ swap₊
    ⇔⟨ re-organize ▣ _ ⟩
      ((id ⊕ c₁) ⊙ (c₂ ⊕ id)) ⊙ swap₊
    ⇔⟨ associativity ⟩
      (id ⊕ c₁) ⊙ ((c₂ ⊕ id) ⊙ swap₊)
    ⇔⟨ _ ▣ swapr ⟩
      (id ⊕ c₁) ⊙ (swap₊ ⊙ (id ⊕ c₂))
    end₂

The formal proof of p₁ ⇔ p₃ can also be shown diagrammatically:

Step 0: preparation.

Step 1: apply idl and idr to c₂ and c₂ respectively with _□₊_, and leave swap₊ alone (_▣_ silently applied).

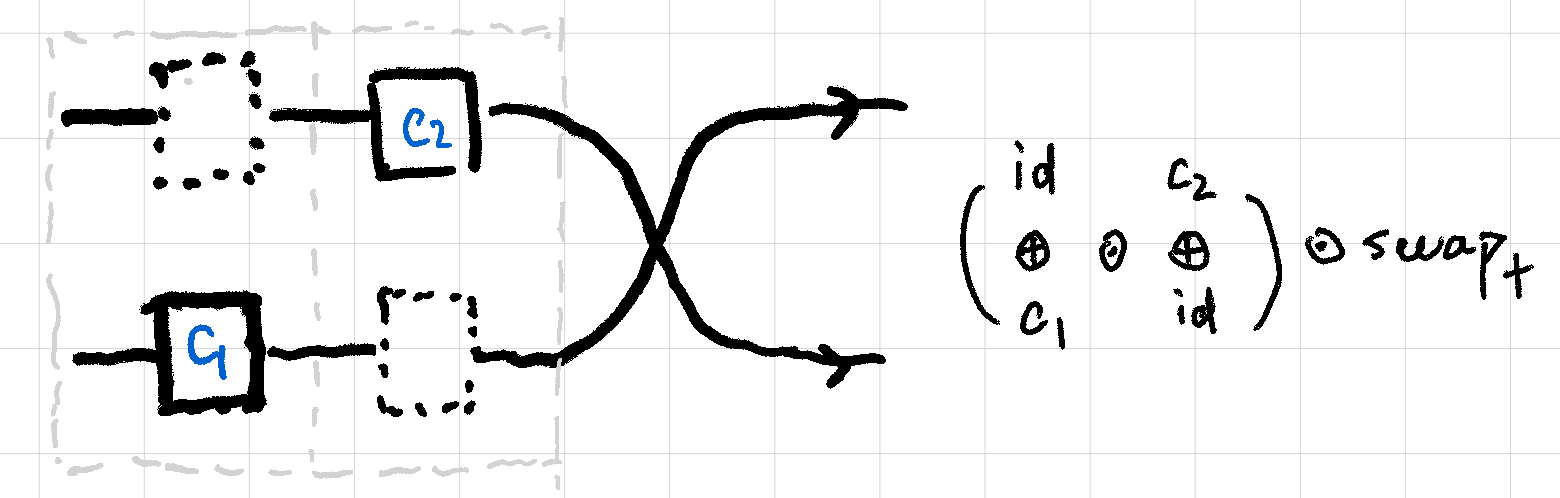
Step 2: re-organize the left part of the program, and leave swap₊ alone (_▣_ applied silently).

Step 3: apply associativity to the whole program.

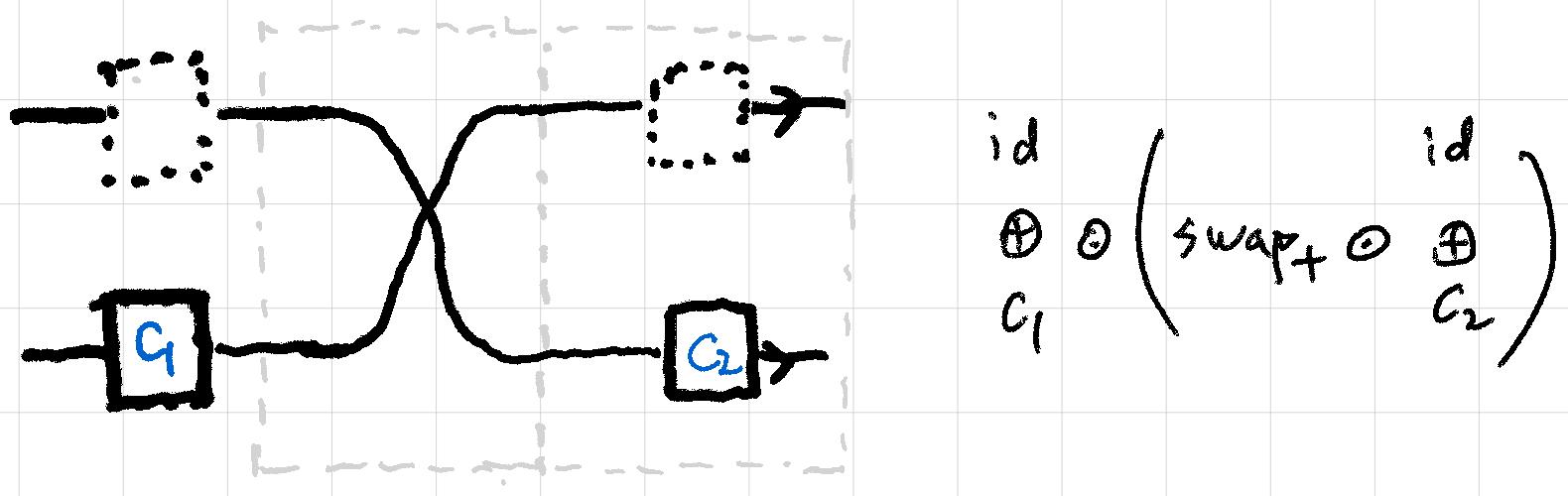
Step 4: apply swapr to the right part of the program, and leave the left part alone (_▣_ applied silently).

↶ Home