UIP as an incarnation of "Being"

I would like to show how UIP can fit into the picture of “From Being To Becoming” in this article.

UIP and its problem

The uniqueness of identity proofs (UIP) principle basically says, if you have two proofs of identity, then these two proofs themselves are always considered equivalent.

A   ∈ Type ℓ
a b ∈ A 
p q ∈ a ≡ b
-----------
UIP ∈ p ≡ q

This can be problematic if a and b have some “structures” and you need to know the information about how a and b are made equivalent. Let’s see a simple example (and you may see this example from many HoTT papers and books) - when a and b are both Bool.

Now imagine we have two proofs of Bool ≡ Bool, namely p and q. By intuition, can you see when p and q should not be considered equivalent?

p q ∈ Bool ≡ Bool

We have four functions in total of type Bool → Bool, and two of them - id and not - are “reversible”:

constT constF id not : Bool → Bool

constT x = true

constF x = false

id true  = true
id false = false

not true  = false
not false = true

Now suppose you don’t know anything specific in HoTT like univalence. The intuition here is: a proof of type Bool ≡ Bool is something like a “reversible program”, and since it’s a program, there has to be some computational, or operational content telling how Bool becomes equivalent to Bool. Therefore, id and not can be viewed as two distinct proofs of Bool ≡ Bool - and that’s something consistent with our “mental model” under most situations.

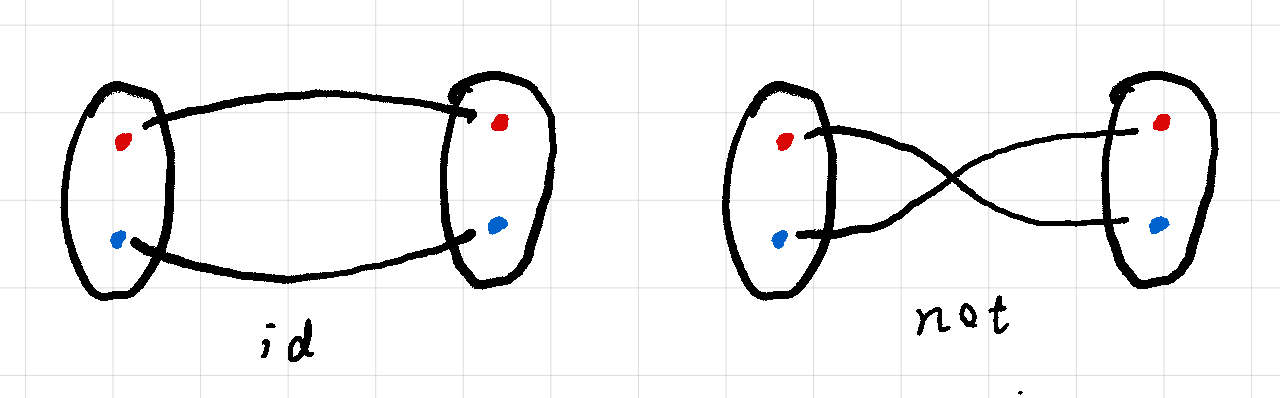
UIP as “Being”

The refutation of UIP has lead to 2DTT and HoTT. Now let me put UIP into the “From Being to Becoming” story. As you have already seen, by accepting UIP as a universal principle, you only get an “yes, it’s proved to be true” answer without any information about “evidence” - that is, the process of finding the truth. You only care about the destination, and forget everything in the journey. Whenever you see an equivalence like X = Y, you only notice “X is Y” and neglect “X becomes Y in some interesting way”.

Where we stop asking “How”

By rejecting UIP, we take one step toward “Becoming”. But we should also notice that, even if we permit distinct identities between elements, like id not ∈ Bool ≡ Bool but id ≠ not, we don’t usually care about how two proofs of identities are equivalent. For example, there are usually more than one ways to prove not ⊙ not ≡ id:

way1 way2 ... ∈ not ⊙ not ≡ id

These “ways” can be different in some sense, but we don’t care. This is the case in 2DTT and Π-family reversible programming languages. I would like to say, where we should stop asking “how” and just focus on “whether or not”, depends on some practical interests. Theoretically, if you keep asking “how”, you will push the “Becoming” worldview to the extreme, and get something called ∞-groupoid.

I thank Prof. Amr Sabry for insightful lectures on Programming Language Foundations.