Type safety of abstract machines, intuitively

To prove type safety of a language, two lemmas - “preservation” and “progress” - are usually involved. They can be less intuitive to people who are not familiar with types. I would like to build a bridge between nanopass compiler framework and proof of type safety of abstract machines.

A nanopass compiler

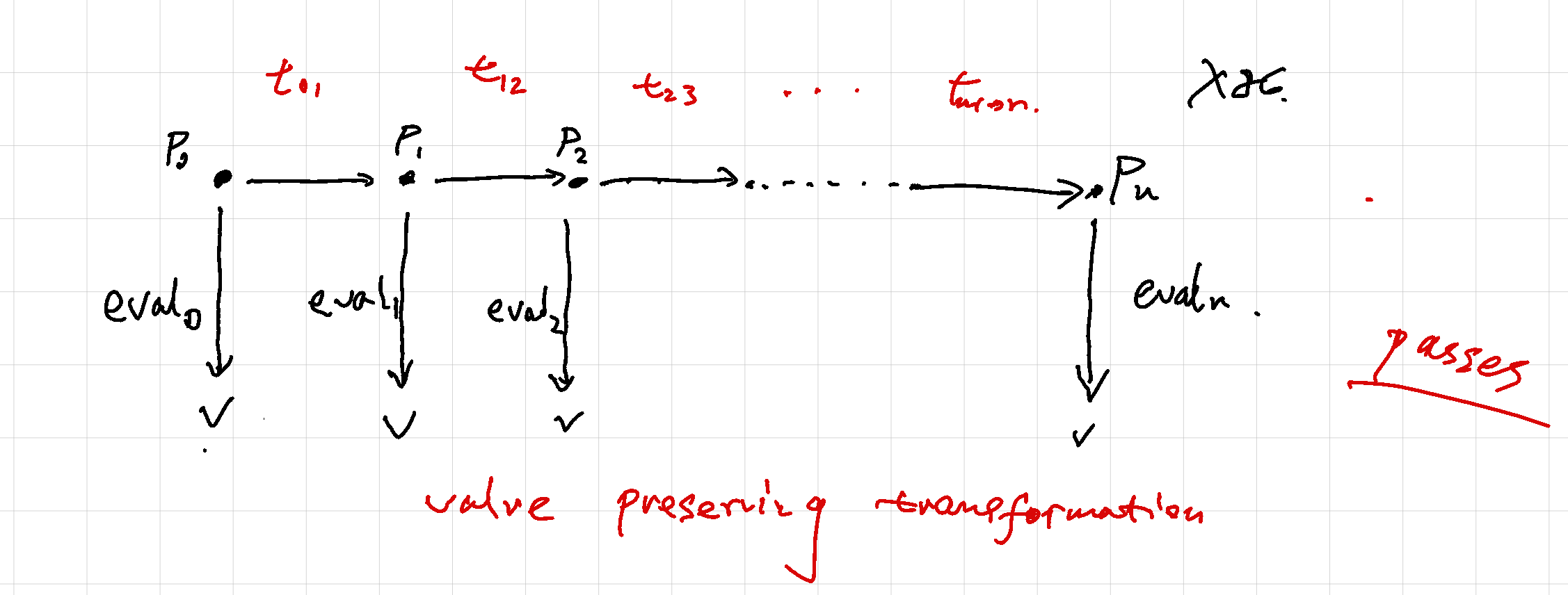
In the above picture, points p₀ p₁ p₂ … pₙ are programs in the source language, IRs, and the target language (e.g. X86); arrows t₁₂ t₂₃ … tₙ₋₁ₙ are compiler passes that transform a program from pₙ₋₁ to pₙ; arrows eval₀ eval₁ … evalₙ are evaluators of the source language, IRs, and the target language.

In a desirable nanopass compiler, each pass should preserve the observable behaviors of the source program. So by evalₓ we can see each program, from source down to the target, is evaluated to have value v. These passes are what I call “value preserving transformations”.

Type Safety of an abstract machine

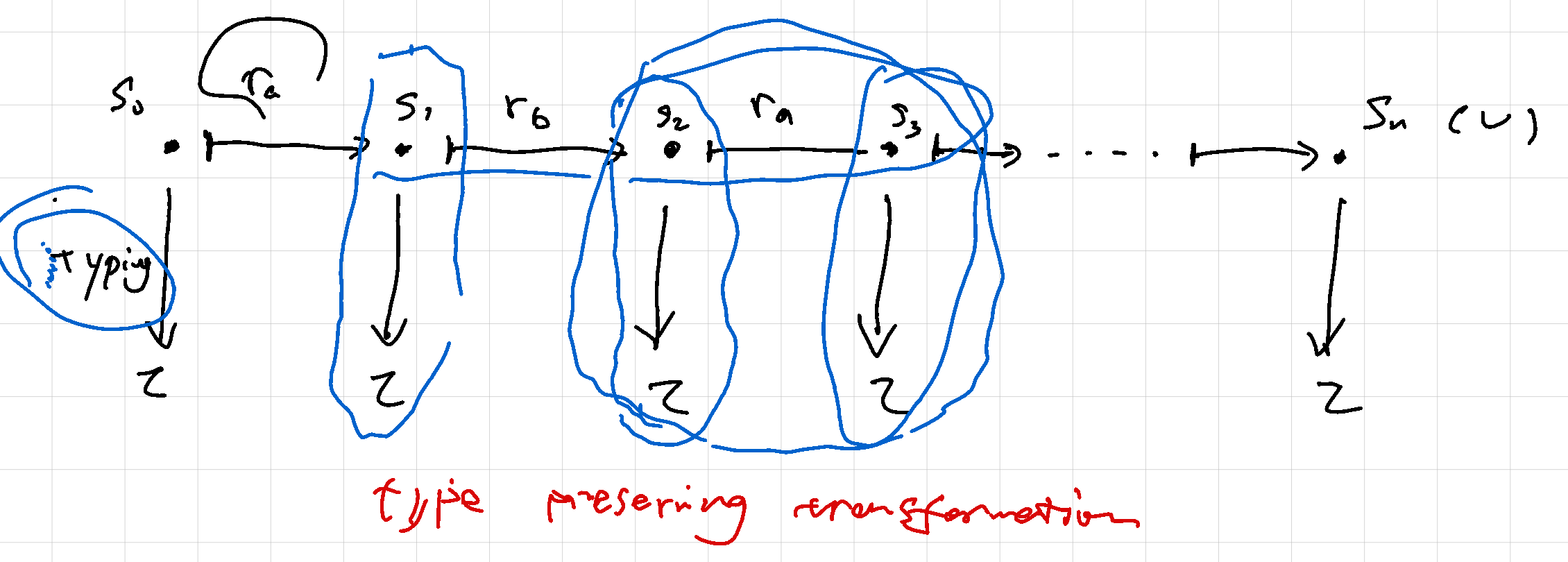
Similarly, points s₀ s₁ … sₙ are machine states from a concrete computation; arrows ra rb … are state transition rules. Now think about the question: what are these vertical arrows mean?

They are of type State → Type, so basically they represent typing of machine states. The proof of machine state typing can be hard and tedious, but luckily it’s off-topic. Now you have the big picture and the informal correspondence, let’s focus on what preservation and progress mean.

• preservation: grab any two adjacent states sₓ and sₓ₊₁, and the arrow between them, say rx. If sₓ ⊢ τ, and rx : sₓ ↦ sₓ₊₁, we should have sₓ₊₁ ⊢ τ as well, i.e. rx preserves the type.
• progress: grab any state sₓ, and its typing sₓ ⊢ τ, then we know sₓ is either the finial state, or there is another state sₓ₊₁ where it can go along the transition rx : sₓ ↦ sₓ₊₁.

By connecting preservation and progress, we can prove that all transition rules preserve typing.

One significant difference here from the compiler example is, each transition rule can be used more than once during the computation while each compiler pass is unique along the whole compilation. These transition rules can also be called “type preserving transformations”.

Questions

1. Can you see the relation between the arrow evalₓ in the first picture and the whole computation s₀ ↦* sₙ in the second picture?
2. Relation to Category Theory and commutative diagrams?